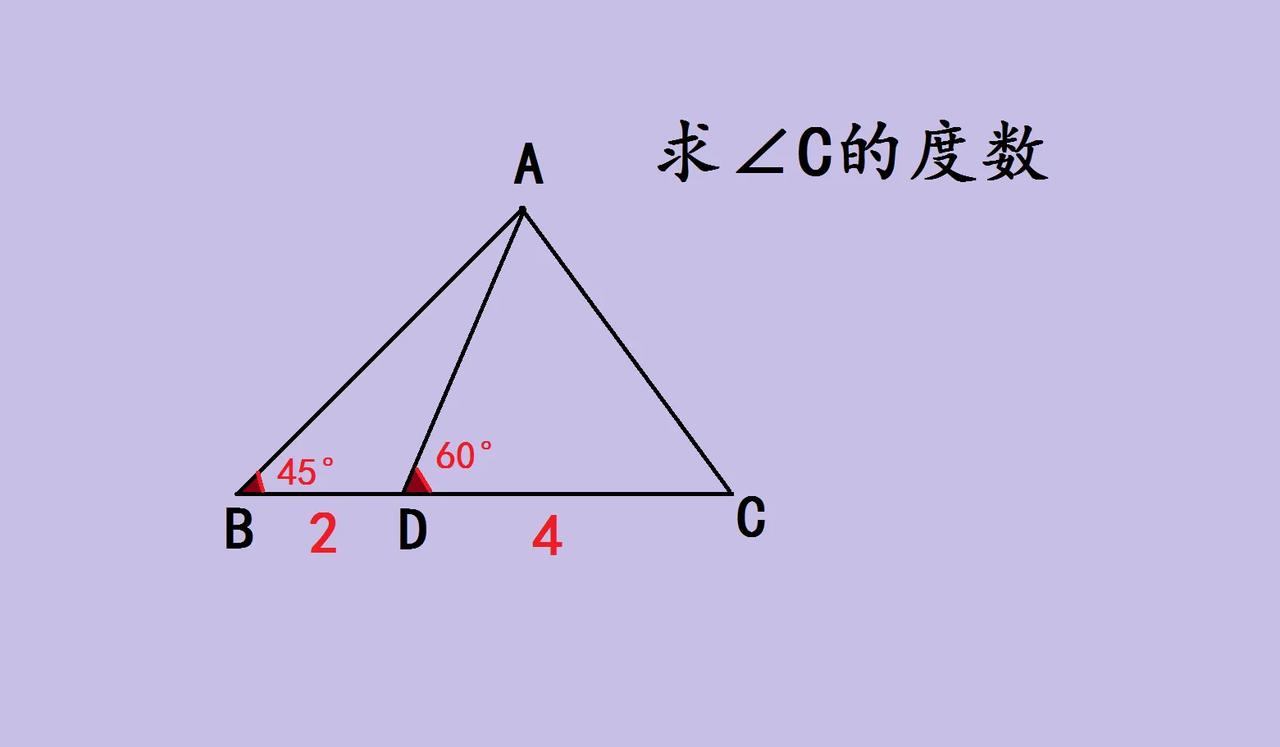
初中几何题，巧用思路破局 刚刷到一道超有意思的初中竞赛几何题，分享下巧妙解法！题目是三角形ABC，BC 上有 D 点，BD=2、DC=4，∠B=45°，∠ADC=60°，求∠C 度数。 解题关键在构造辅助线！过 A 作垂线，或利用角度关系找特殊三角形？其实，我们可以用“截长补短”结合角度转化。观察到∠ADC=60°，若从 D 作辅助线，构造含 60°的特殊三角形，比如等边三角形，把线段和角度关联起来。 当把 BD、DC 的长度比（1:2）与角度结合，通过构造圆或利用正弦定理（不过初中阶段可借助几何直观），能发现角之间的传递关系。45°与 60°的角，经过辅助线构造，让隐藏的角度显现，从而推出∠C 的度数。 这类题考验知识融合，把三角形基本性质、角度推导和巧妙辅助线结合，打破常规思维。初中竞赛常藏这种“小陷阱”，但找到突破口就超有趣，刷题的成就感这不就来了！大家遇到几何题别慌，多试试构造法，说不定就柳暗花明～
猜你喜欢
【4评论】【1点赞】
【1评论】
【2评论】【1点赞】
【49评论】【20点赞】
【2评论】【33点赞】
作者最新文章
热门分类