​​

“难度太大、全军覆没在所难免！”这是一道九年级数学测试压轴题：仅知底部对应角度值、及其上中线长，咋求三角形面积最大值？

如图，

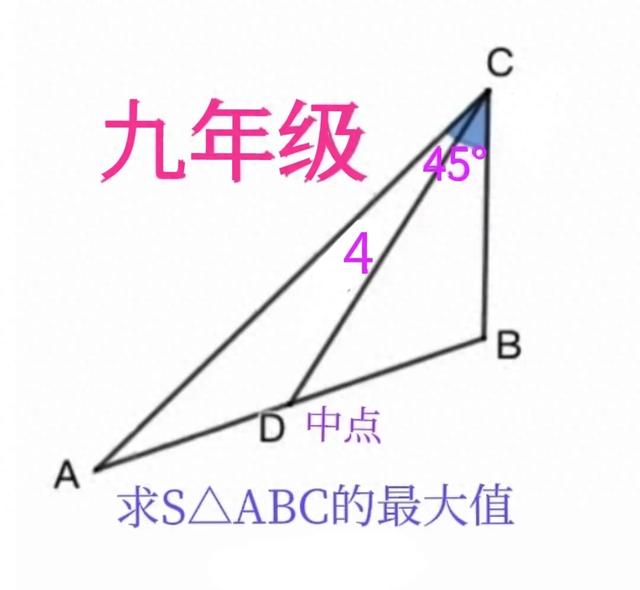
在△ABC中，∠ACB=45°，CD为AB上中线且CD=4，求三角形ABC面积的最大值。

解题方向：①将S△ABC转化成“至少有一条定边和一个定角”三角形的面积②利用定边和定角关系，作外接圆，并求定边上高的最大值。

提示：三角形全等+等积代换+外接圆！

①延长CD至点E，使得CD=DE，连接AE和BE，则BE=8，△ACD≌△BED，故∠CBE=135°，S△ABC=S△BCE。

②作△BCE的外接圆O，由∠CBE=135°可知弦BE另一侧圆周角为45°，从而圆心角为90°。

③连接OC与OE，则OCE为等腰直角三角形，从而圆O半径OC=OE=4√2。

④过点B作CE的垂线CF，则CF≥4√2-4等号成立当且仅当B、O、F三点共线，故△BCE底边CE上高的最大值为4√2-4，此时

S△ABC=S△BCE=(4√2-4)×8÷2=16√2-16。

———————————

友友们，怎么看？欢迎留言分享！