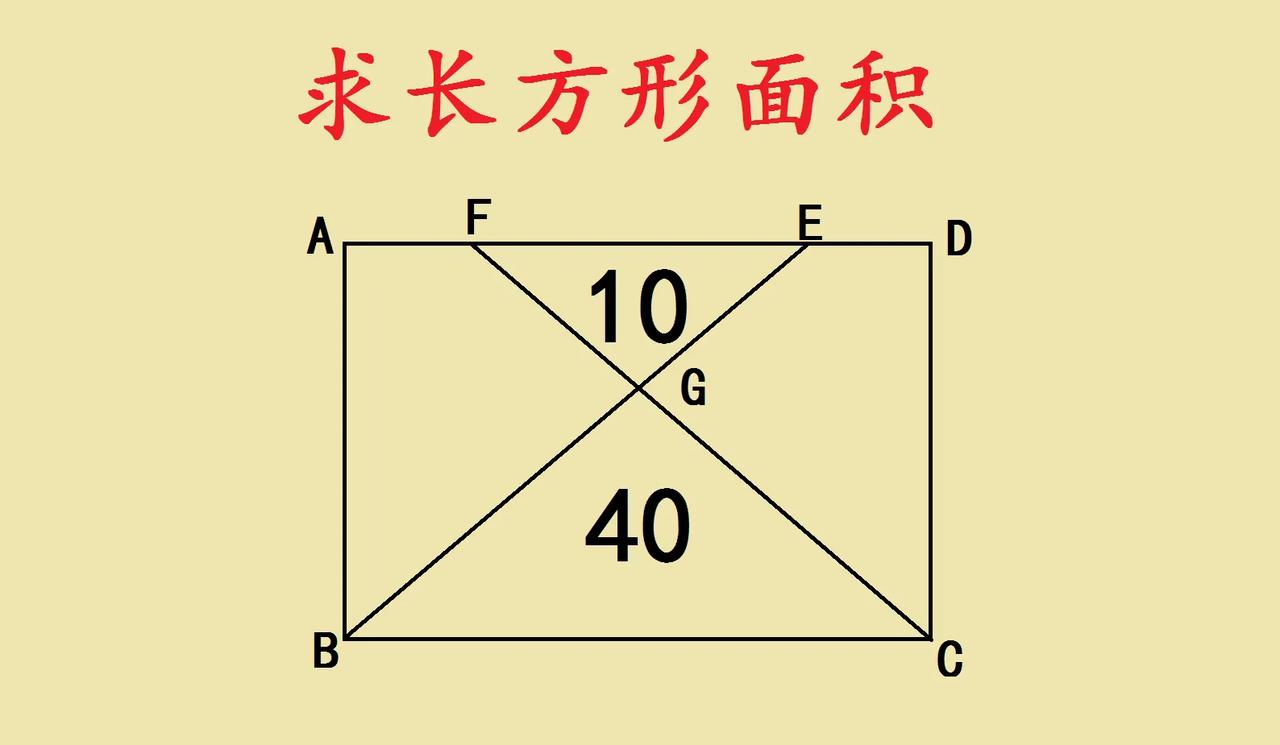
五年级附加题，求长方形面积，图里的线段关系暗藏玄机。 长方形ABCD中，F、E在AD上，连接BF、CE，相交于G，三角形EFG面积10，三角形BCG面积40 。这时候得调动几何知识，利用长方形对边平行（AD平行BC ），能发现三角形EFG和三角形BCG是相似三角形。相似三角形面积比是边长比的平方，算下面积比10:40 = 1:4，那边长比就是1:2 。 接着看，借助这个相似关系，再结合长方形里的三角形面积特性，能找到和长方形面积相关的联系，把这些线段、面积关系串起来，就能巧妙算出长方形面积啦。几何题就像这样，把零散的条件通过定理织成网，一步步推导超有成就感，玩懂几何，就像解锁思维解谜游戏，越钻研越上头，大家也试试这种奇妙的几何探索呀！
先拉线，吧f点拉倒a点.e点拉倒d点。正好是4个对称三角形组成的长方形。上下2个三角洲正好是面积一半。再次拉线，合并f和e到中间点。中间三角洲正好也是面积一半，上面三角洲可以看做无限小任然存在，。 因此得出结论，在cf.be相交对称时上下三角形必然是面积的一半，面积就是40+10+40+10
![为什么“唯独汉字停止了演化”？首先汉字一直在演化。[吃瓜]](http://image.uczzd.cn/1100864438958548486.jpg?id=0)
用户18xxx86
5年级你说相似三角形？那是7年级的好吗？
战斗鸡 回复 06-22 20:17
6年级就有了
赵追
蝴蝶定理。120
左右 回复 06-22 20:56
对了，需要先根据沙漏模型得出EF＝½AD
左右 回复 06-22 20:55
连接AG和DG就是一个一半模型，（20+40）✖️2＝120。
左右
我很好奇给你点赞的都是些什么人。