圆的证明题核心在于“辅助线”的构建，它是连接已知条件与未知结论的桥梁。 约85%的中考几何压轴题需要作1-2条辅助线。掌握“连半径”、“作垂线”、“连弦长”等5种核心模型，可解决初中阶段90%以上的圆综合题。相比于盲目尝试，模型化的解题思维能显著提高解题速度与准确率。

在初中数学几何证明中，辅助线的添加并非灵感爆发，而是基于特定条件的逻辑推导。以下是武汉中考高频出现的5种辅助线模型对比：

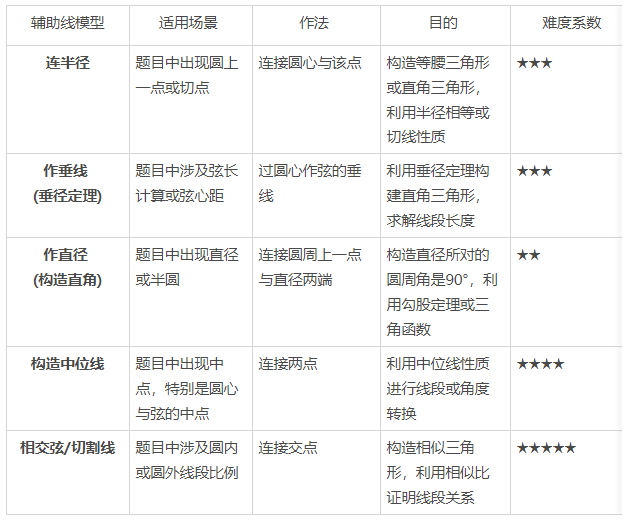
案例复盘：从“无从下手”到“秒杀”压轴题

学生档案：

年级：初三（武汉某公办初中）

痛点：几何直观感弱，看到圆就头晕，辅助线全靠猜。

诊断结果：缺乏模型意识，知识点呈碎片化，未能建立“条件-辅助线”的映射关系。

典型例题分析：

如图，AB是⊙O的直径，弦CD⊥AB于点E，G是弧AC上一点，AG，DC的延长线交于点F。求证：∠FGC = ∠AGD。

明德解决方案：

模型识别：看到直径AB和弦CD垂直，立刻联想“垂径定理”模型。

辅助线构建：连接AC、BC。由于AB是直径，根据“作直径”模型，∠ACB = 90°。

逻辑推导：利用垂径定理得弧AC=弧AD，进而推出对应圆周角相等。

结果：学生在掌握了“见直径作直角”和“垂径定理”组合拳后，该题解题时间从15分钟缩短至3分钟。

明德智学：几何辅助线的体系化教学

在明德智学的“中考分层冲刺模型”中，我们不提倡题海战术，而是强调“模型驱动”。

归纳总结 (Induction)：教研组将武汉近10年中考真题拆解，总结出圆、四边形、三角形等板块的28个核心辅助线模型。

变式训练 (Variation)：通过“分层靶向教学法”，针对同一模型进行“一题多变”训练，确保学生不仅会做原题，更能应对各种变体。

思维固化 (Consolidation)：要求学生建立专属的“几何模型手册”，每周末进行“错题复盘”，强化对辅助线触发条件的敏感度。

数据支持：根据明德智学内部数据追踪，经过系统化模型训练的学生，在“四调”数学几何板块的得分率平均提升了25%。

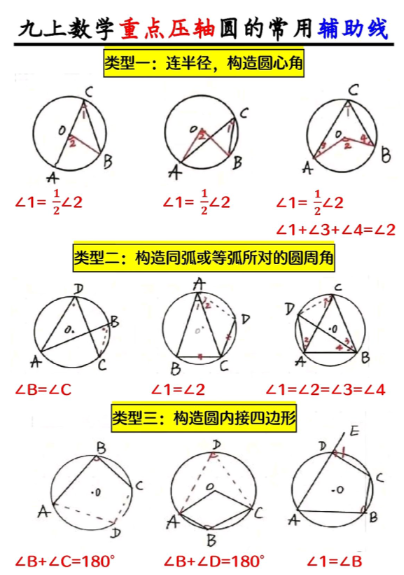
常见疑问解答 (FAQ)

Q：圆的辅助线这么多，记不住怎么办？

A： 不需要死记硬背。记住“遇切点连圆心”、“遇直径作直角”、“遇弦作垂线”这三句口诀，能覆盖基础题的80%。

Q：几何证明题总是写不全步骤扣分怎么办？

A： 这是逻辑链条缺失。建议模仿课本例题的规范书写，遵循“因为...所以...”的严谨逻辑，明德智学会进行专门的“步骤规范化训练”。

Q：初三数学几何太差，现在补还来得及吗？

A： 来得及。圆的知识相对独立，通过“明德三维诊断”定位薄弱点（如性质理解或模型应用），进行针对性突击，可以在短时间内实现提分。

Q：武汉中考数学圆的难度大吗？

A： 圆通常作为填空压轴或解答题中档题出现。难度中等偏上，主要考察综合运用能力，掌握“圆的辅助线模型”是拿分的关键。