在矢量微积分和物理学中，梯度、散度和旋度是描述场（场的分布）行为的三大核心算子。它们如同三根支柱，共同支撑起我们分析电磁场、流体力学等问题的数学框架。理解它们，不仅在于记住公式，更在于把握其背后的几何与物理图景。

1. 它是什么？梯度（Gradient）是标量场的导数。它将一个标量场（如温度、海拔）映射为一个矢量场。

2. 物理意义：方向与速率

方向： 梯度矢量的方向指向标量场增长最迅速的方向。

大小： 梯度矢量的模长表示在该方向上的变化率。

想象一下： 你身处一片起伏的山丘。你手中的地图是海拔标量场。

梯度就是一个箭头，精准地指向你所在位置最陡的上坡方向。

箭头越长，代表那个方向的山坡越陡。

3. 数学公式（三维）

4. 记忆口诀

“标量求导变成矢” —— 对一个标量函数求梯度，结果是一个矢量。公式就是三个偏导数组成的矢量。

1. 它是什么？散度（Divergence）是矢量场的一种度量。它将一个矢量场映射为一个标量场。

2. 物理意义：源与汇

正散度： 表示该点是场的 “源” ，场线从这里发散出去（如正电荷、水龙头）。

负散度： 表示该点是场的 “汇” ，场线在这里汇聚消失（如负电荷、地漏）。

零散度： 表示该点既无源也无汇，场线只是穿过（如不可压缩流体的稳定流动）。

想象一下： 一个水流场。

在水龙头处，水向外喷出，散度为正。

在地漏处，水被吸走，散度为负。

在平稳的河道中，流入和流出的水量相等，散度为零。

3. 数学公式（三维）

4. 记忆口诀

“矢量点乘变成标” —— 两个矢量（∇ 和 F）点乘的结果是一个标量。公式是“自己对自己求导再求和”（Fx 对 x 求导，等等）。

1. 它是什么？旋度（Curl）也是矢量场的一种度量。它将一个矢量场映射为另一个矢量场。

2. 物理意义：旋转的强度与轴

方向： 旋度矢量的方向遵循右手定则，表示场在该点旋转的轴方向。

大小： 旋度矢量的模长表示场在该点的旋转强度。

想象一下： 一个漩涡或龙卷风。

在漩涡中心，水流或气流在剧烈旋转。此处的旋度很大。

旋度矢量的方向垂直于旋转平面，用右手定则判断（四指弯曲方向为场旋转方向，拇指方向为旋度方向）。

3. 数学公式（三维）

4. 记忆口诀

“矢量叉乘还是矢” —— 两个矢量（∇ 和 F）叉乘的结果仍然是一个矢量。用行列式法记忆最方便，或记住循环顺序（x->y->z->x）：每个分量的正项是“下一个”变量的偏导。

为了更清晰地把握，我们将三者置于同一张表格中进行对比：

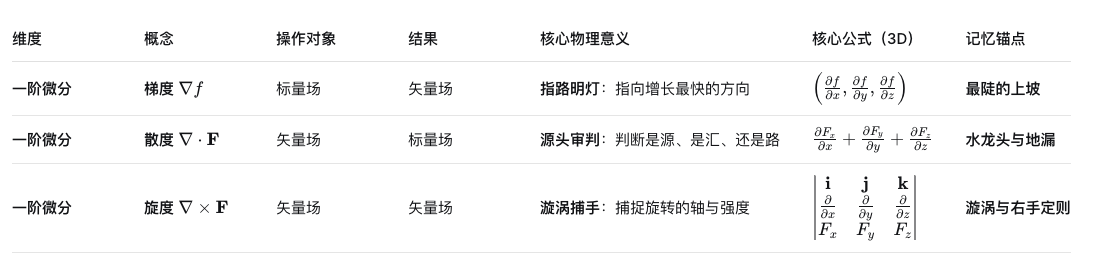
它们的内在关联：

“旋度无源”：一个矢量场的旋度场，其散度必然为零（∇⋅(∇×F)=0）。这意味着漩涡本身没有源头，漩涡线永远是闭合的圈，不会突然从某一点冒出来。

“梯度无旋”：一个标量场的梯度场，其旋度必然为零（∇×(∇f)=0）。这意味着最陡的山坡路径本身是不会旋转的，它是“保守场”的标志。

梯度、散度和旋度并非孤立的数学符号，它们是解读自然界各种场现象的“语言”。通过梯度，我们知晓场变化的趋势；通过散度，我们洞察场产生的根源；通过旋度，我们感知场内在的旋转。将公式与生动的物理图像结合，你便能真正地理解、记忆并灵活运用这三把开启矢量世界大门的钥匙。